Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
- цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9);
- буквы латинского и греческого алфавитов ((a, b, c, d, α, β, γ, δ) и т.д.)
- знаки математических действий ( (+, -, times , div), и т.д.);
- скобки (), [], <>.
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
- 258 – конкретное числодвести пятьдесят восемь;
- (a + b) – сумма любых двух чисел;
- (x + 24 = 78) – уравнение с неизвестным первым слагаемым икс.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
- числа, обозначенные цифрами или буквами,
- знаки математических действий, которые связывают эти числа математическими действиями;
- вспомогательные знаки – скобки.
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
- x;
- 74;
- (2cdot3)
- (adiv (25+38))
- (374+(48cdot 2))
- (ac + bc)
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
- запись только знака;
- запись, не обозначающая математического действия над числами (когда знаки не связывают собой числа и не указывают на последовательность действий);
- запись, в которой присутствуют знаки сравнения (в этом случае запись является уравнением или неравенством, сравнивающем два и более выражений).
Например, это НЕ математические выражения:
- (
- +
- ((div 8-59)
- (35cdot 12(+74)
- (a+5=12)
- (38+87<25cdot x)
- ((1000+x)div 2=784)
Числовое значение выражения – это число, которое получается в результате выполнения всех действий в правильном порядке, указанных в данном выражении.
Найти числовое значение выражения – это означает совершить все арифметические действия, записанные в выражении, в правильном порядке, и получить число, являющееся значением данного выражения.
Например:
((35+4)cdot 2) — это выражение, а 78 — это числовое значение этого выражения, полученное в результате выполнения всех арифметических действий этого выражения.
- Виды математических выражений
- Случаи опускания знака умножения в выражениях
- Как читать математические выражения
- Алгоритм чтения математических выражений
- Формулы
- Что такое глагол в русском языке?
- Глаголы в русской речи
- Неопределенная форма глагола
- Переходные и непереходные глаголы
- Возвратные и невозвратные глаголы
- Вид глагола
- Спряжение глаголов
- Наклонение
- Время у глаголов
- Лицо у глаголов
- Безличные глаголы
- Морфологические признаки глагола
- Синтаксическая роль глагола
- Видеоурок «Глагол как часть речи»
- Заключение
- Математические действия на английском языке
- Основные математические действия на английском: сложение, вычитание, умножение и деление
- Дроби на английском языке
- Простые дроби – common fractions
- Десятичные дроби – decimal fractions, decimals
- Проценты в английском языке, трудности с числом глагола
- Возведение в степень в английском
- Математические выражения со скобками
- Карточки с английскими словами на тему “Математика”
Видео:Что такое глагол?Скачать

Виды математических выражений
Числовые – выражения, которые состоят только из чисел, выраженных цифрами, и знаков: (5+3; 28div 4; 32cdot (25+15));
Буквенные – выражения, которые состоят из чисел, выраженных и цифрами, и буквами, или только буквами, и знаков: (5cdot a; a+b; 64div (2+c)).
Видео:Что такое глагол? Глагол как часть речиСкачать

Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
- между числовым и буквенным множителем: (5cdot x = 5x)
- между буквенными множителями: (acdot b = ab)
- между числовым множителем и скобкой: (3cdot (d+c)=3(d+c))
- между буквенным множителем и скобкой: (acdot (b+c)=a(b+c))
Видео:Математика это не ИсламСкачать

Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
- (2+3) – суммачисел 2 и 3
- (5cdot 4) – произведение чисел 5 и 4
- (24div 6) – частноечисел 24 и 6
- (35-5) – разность чисел 35 и 5
Более сложные выражения, называют по последнему выполняемому действию:
- ((a+b)-c) – разность суммы чисел a и b и числа c
- ((a+b)cdot (a-b)) – произведение суммы чисел a и b и разности чисел a и b
- (adiv (ccdot d)) – частное числа a и произведения чисел c и d
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
- Сумма первых пяти натуральных чисел – (1+2+3+4+5)
- Произведение всех однозначных чисел – (1cdot 2cdot 3cdot 4cdot 5cdot 6cdot 7cdot 8cdot 9)
- Сумма всех двузначных чётных чисел – (10+12+14+…+94+96+98)
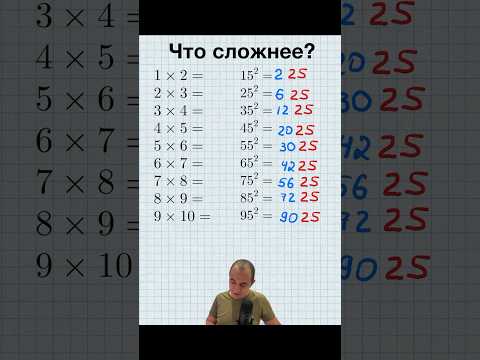
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
- Определить порядок действий в выражении
- Прочитать, начиная с последнего действия
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
- (35cdot (28-12)) – Произведение числа 35 и разности чисел 28 и 12
- (35cdot (28-12)+64) – Сумма произведения числа 35 с разностью чисел 28 и 12, и числа 64.
- (35cdot (28-12)+64–32div 16) – Разность суммы произведения числа 35 и разности чисел 28 и 12 с числом 64, и частного чисел 32 и 16
Видео:Глаголы с дефектом! Вы про них знаете? Какие глаголы называют недостаточными? | Русский языкСкачать

Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью (v_) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: (v_=3cdot v_);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: (v_
= v_-15).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
Видео:Что такое математические структуры? Душкин объяснитСкачать

Что такое глагол в русском языке?
Глагол — это самостоятельная часть речи, которая имеет характерные постоянные и непостоянные признаки, отличающие его от слов других частей речи: вид, переходность, возвратность, спряжение и т. д.
В системе частей речи русского языка существуют слова, которые обозначают действие (стелить), процесс (объяснять), состояние (чувствовать). Такие слова называют глаголами.
Видео:Спряжение глаголов. Как определить спряжение глаголов?Скачать

Глаголы в русской речи
Многие лингвисты считают, что глагол – самая сложная и самая емкая часть речи, которая обладает широкими возможностями описания жизни в ее развитии, движении . А. Н. Толстой писал:
Найти верный глагол для фразы – это значит дать движение фразе.
На удивительную силу русского глагола обращали внимание многие писатели и языковеды. Например, Николай Греч писал:
Глагол придает речи жизнь, — присутствием своим животворит отдельные слова.
Термин «глагол» восходит к старославянскому слову «глаголить», что по-русски значит «говорить». В древнерусском языке одним из значений лексемы «глагол» было «слово», «речь вообще». Именно в этом смысле употребил его А.С. Пушкин в стихотворении «Пророк»:
Глагол — это важнейшая часть речи в русском языке. Уже в самом названии подчеркивается его особая значимость.
Глагол как часть речи обозначает «процесс». С помощью глагола мы узнаем, как все в этом мире двигается, говорит, меняет краски, как звучит, как чувствует себя.
Известный русский лингвист А.М. Пешковский утверждал, что «глаголы — это слова, оживляющие все, к чему они приложены». И это действительно так.
С помощью имен существительных можно назвать предметы и явления, которые нас окружают. Имена прилагательные помогают уточнить то, что названо именем существительным, но только глаголы могут «оживить» окружающий нас мир.
Языковедами глагол выделяется как самая сложная и ёмкая самостоятельная часть речи. По подсчетам ученых глагол занимает второе место (после существительного) по частоте
употребления в речи.
Чтобы понять, что такое глагол в русском языке, рассмотрим его общее грамматическое значение, морфологические и синтаксические признаки. А начнем мы с определения:
Видео:таблица умножения школаСкачать

Неопределенная форма глагола
Неопределенная форма (инфинитив) является исходной, начальной формой глагола и отвечает на вопросы
что делать? что сделать?
Глаголы в неопределенной форме заканчиваются на -ть, -ти и -чь:
Запомним неопределенную форму глагола «прийти» (ср. «зайти», «выйти», «отойти», «обойти» и пр.)
Начальная форма не обозначает времени, не имеет непостоянных признаков лица или числа. Она имеет только вид, может быть переходным или непереходным, возвратным или невозвратным.
Синтаксическая функция неопределенной формы шире, чем у других форм глагола. Инфинитив может выступать в роли всех членов предложения.
Выдать чужой секрет — предательство , выдать свой — глупость (Ф. Вольтер).
Успеха можно добиться , если приложить старания.
Искусство (какое?) говорить не каждому дано.
Отец не разрешает сыну (что?) открывать дверцу птичьей клетки.
Дети пришли (с какой целью?) посмотреть на новорожденных котят.
Глаголы выражают действие или состояние в грамматических формах вида, переходности, наклонения, времени, лица и числа и пр. Рассмотрим, какие постоянные признаки имеет глагол как самостоятельная часть речи.
Видео:Спряжение глаголов | Русский язык |TutorOnlineСкачать

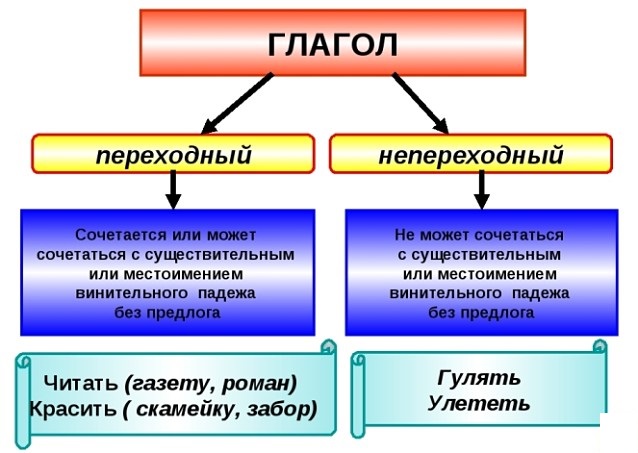
Переходные и непереходные глаголы
В русском языке глаголы делят на переходные и непереходные. Переходные глаголы обозначают действие, которое переходит на предмет. Грамматически это выражается в их способности управлять
- формой винительного падежа существительного (местоимения) без предлога (защититьРодину);
- формой родительного падежа, обозначающей часть от целого, либо при отрицании (попробовать сока, не дождаться известия).
Все остальные глаголы, управляющие существительными с предлогами, в том числе возвратные глаголы, являются непереходными:
- стоять на пороге;
- подойти к нему;
- сомневать ся .
Видео:#200. ЗАЧЕМ НУЖНА МАТЕМАТИКА?Скачать
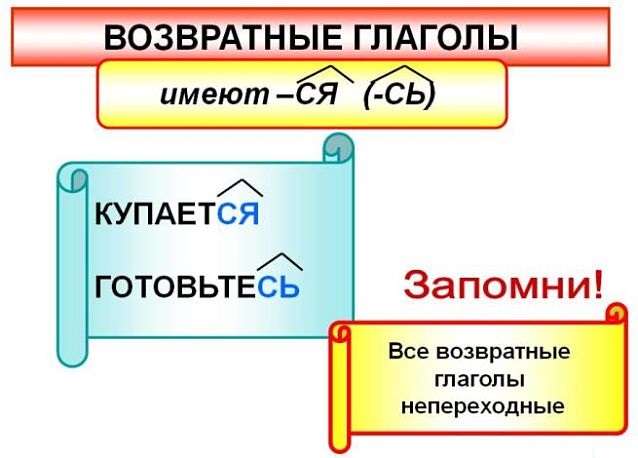
Возвратные и невозвратные глаголы
Возвратность является постоянным грамматическим признаком глаголов. Возвратные глаголы обозначают, что действие переносится на само действующее лицо:
- улыбается, умывается, построиться;
- нестись, пройтись.
Показателем возвратности является наличие в конце слова постфикса -ся /-сь.
Видео:Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

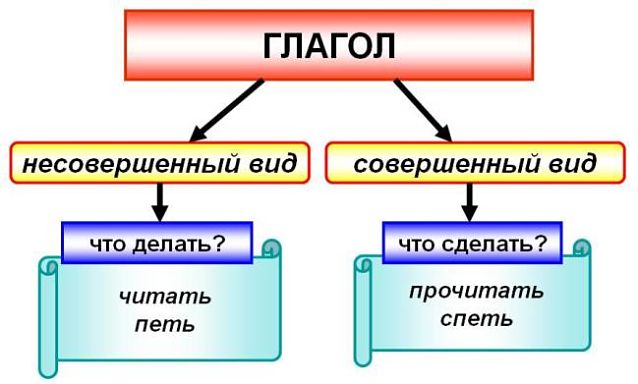
Вид глагола
Вид глагола — это постоянный грамматический признак слов этой части речи.
Все глаголы распределяются на две группы в зависимости от того, как протекает действие, обозначенное ими:
- глаголы совершенного вида;
- глаголы несовершенного вида.
Глаголы совершенного вида связаны с достигнутым результатом действия, его началом или концом или с однократностью действия (глаголы с суффиксом -ну-). Эти слова отвечают на вопрос что сделать?
Они имеют только две формы времени:
- прошедшее (обозначил, заиграл, капнул);
- будущее простое (обозначим, отложишь, пролает).
Глаголы несовершенного вида обозначают длительное, совершающее в данный момент или повторяющееся действие и отвечают на вопрос что делать?
Эти слова имеют три формы времени:
- настоящее (рисует, поешь, танцуем);
- прошедшее (рисовал, пел, танцевал);
- будущее сложное (буду рисовать, будешь петь, будут танцевать).
Видео:Времена глаголов. Как определить время глагола?Скачать

Спряжение глаголов
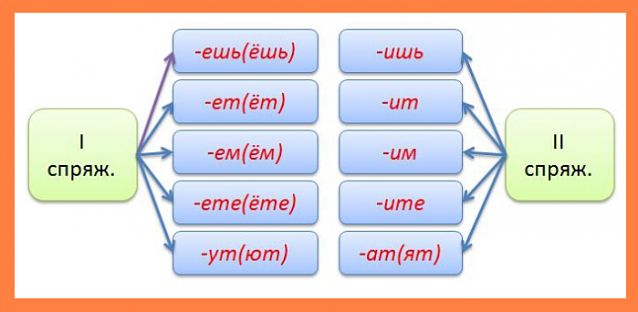
В зависимости от личных окончаний в русском языке различают I и II спряжение глагола.
Личные окончания глаголов I спряжения
Лицо
Окончания
Примеры
Ед. ч.
Мн. ч.
Ед. ч.
Мн. ч.
Личные окончания глаголов II спряжения
Лицо
Окончания
Примеры
Ед. ч.
Мн. ч.
Ед. ч.
Мн. ч.
Глаголы «хотеть» и «бежать» относятся к разноспрягаемым глаголам. Часть личных форм имеют окончание первого спряжения, часть второго:
| Лицо | Хотеть | Бежать | ||
|---|---|---|---|---|
| Ед. число | Мн. число | Ед. число | Мн. число | |
| 1-е | я хочу | мы хотим | я бегу | мы бежим |
| 2-е | ты хочешь | вы хотите | ты бежишь | вы бежите |
| 3-е | он хочет | они хотят | он бежит | они бегут |
Глаголы «есть», «дать» имеют особые личные окончания.
Перейдем к непостоянным признакам глагола.
Видео:🥐как быстро выучить стих🥐Скачать

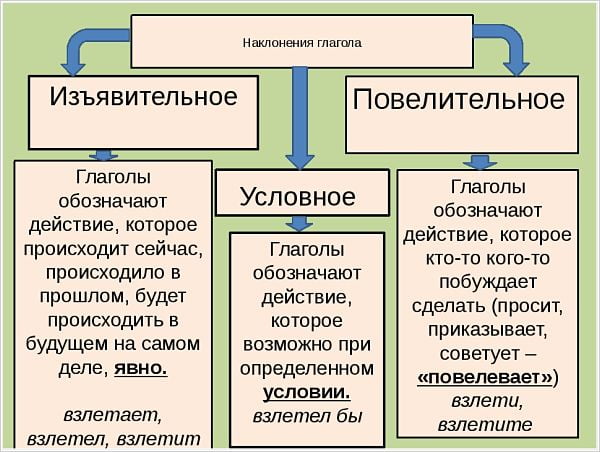
Наклонение
Глаголы употребляются в формах трех наклонений:
- изъявительного
- повелительного
- условного
Изъявительное наклонение обозначает, что действие рассматривается как реальный факт. Оно может происходить в настоящем, будущем или прошедшем времени. Глаголы несовершенного вида в изъявительном наклонении имеют формы всех трех времен:
- стелет (наст.);
- стелил (прош.);
- будет стелить (буд.)
У глаголов совершенного вида существуют формы двух времен:
- спросил (прош.);
- спросит (буд.)
Этим изъявительное наклонение отличается от других наклонений, у которых нет категории времени.
Повелительное наклонение выражает побуждение к действию в виде просьбы, совета, приказа, пожелания. Глагол в повелительном наклонении отвечает на вопросы что делай (те)? что сделай(те)?
Повелительное наклонение образуется с помощью суффикса -и или нулевого суффикса от основы настоящего (будущего времени). Глаголы в форме повелительного наклонения имеют формы единственного и множественного числа:
- ползти — полз ут — полз и , полз и те ;
- сидеть — сид ят — сядь, сядь те .
Условное (сослагательное) наклонение обозначает, что действие возможно при определенных обстоятельствах.
Если ты не поддержала бы меня в тот момент, вся наша затея закончилась бы полным провалом.
Условное наклонение глагола образуется прибавлением частицы бы к форме прошедшего времени. Глаголы в форме условного наклонения изменяются по родам и числам:
- обнадёжить — обнадёжил бы;
- обнадёжил а бы;
- обнадёжил о бы;
- обнадёжил и бы.
Категории времени эти глаголы не имеют.
Видео:Все про глагол. Вид, залог, спряжение, наклонение, время, возвратность, переходность, разборСкачать

Время у глаголов
Время — это непостоянный признак глагола. Различают настоящее, прошедшее и будущее время только у глаголов в форме изъявительного наклонения:
- пишу, пишем, пишете;
- писал, писала, писали;
- будет писать.
Настоящее время выражается посредством личных окончаний глаголов (-ю, ешь, -ет и пр.) и обозначает действие, которое совершается в этот момент или как постоянное свойство предмета:
- мальчик рисует;
- серебро плавится;
- Земля вращается.
Прошедшее время глагола указывает, что действие уже состоялось. Формы прошедшего времени образуются прибавлением суффикса -л- к основе неопределенной формы и окончаний рода и числа:
- краси ть — краси л ;
- указа ть — указа л а ;
- состави ть — состави л о ;
- реши ть — реши л и .
Будущее время обозначает, что действие совершится после момента речи о нем. Формы будущего времени бывают простые и сложные. Простое будущее время имеют глаголы совершенного вида с приставкой:
- написать — напишу;
- оповестить — оповестим.
Сложное будущее время глаголов несовершенного вида образуется с помощью вспомогательного глагола «быть» в личных формах и неопределенной формы:
- буд у готовиться;
- буд ешь стараться;
- буд ет улыбаться и т. д.
Видео:Математическая хитрость для олимпиадников. #математика #хитрость #счет #арифметика #репетиторСкачать
Лицо у глаголов
Грамматическая форма лица обозначает отнесенность действия к определенному производителю. У глаголов различают три формы лица единственного и множественного числа.
Форма 1 лица выражает, что действие совершает сам говорящий (я рисую, мы рисуем).
Форма 2 лица показывает, что действие производит собеседник (ты поешь, вы поете).
Форма 3 лица обозначает, что действует тот, о ком идет речь (он плавает, они плавают).
Значение лица выражается с помощью личных окончаний в настоящем и будущем времени глаголов изъявительного наклонения и личных местоимений:
- я пиш у , напиш у ;
- ты сме ёшь ся, рассме ёшь ся;
- он зов ет , позов ет и т. д.
Безличные глаголы
В русском языке существуют глаголы, которые обозначают действие или состояние человека и природы, протекающее само по себе, без непосредственного деятеля. Это безличные глаголы, которые по грамматической форме совпадают с глаголами третьего лица единственного настоящего и будущего времени или среднего рода в форме прошедшего времени.
Понаблюдаем:
- нездоровится, вечереет, смеркается;
- рассвело, подморозило, запахло.
Некоторые личные глаголы могут употребляться в роли безличных:
- дятел стучит — стучит в висках;
- лес темнеет вдали — темнеет в глазах.
Видео:7 класс, 2 урок, Что такое математический языкСкачать

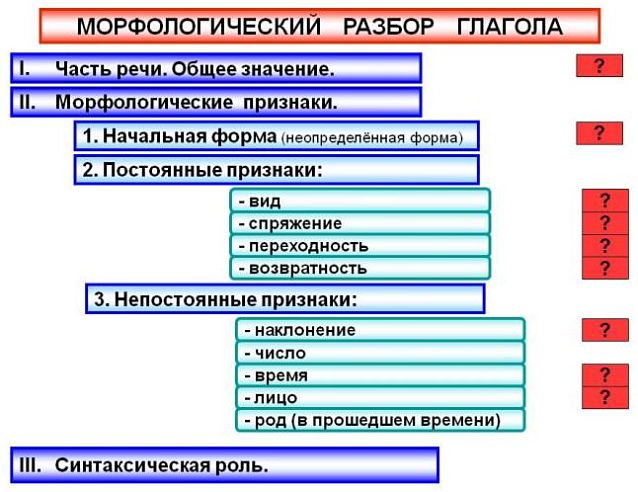
Морфологические признаки глагола
Подытожив исследование глагола как части речи, укажем его грамматические признаки.
Начальная форма — инфинитив.
Постоянные признаки глагола:
I. вид совершенный или несовершенный;
Непостоянные признаки глагола:
II . время (если есть);
III . лицо (если есть);
Видео:Спряжение глаголов. Что такое спряжение глаголов в русском языке? Для чего нужно спряжение глаголов?Скачать

Синтаксическая роль глагола
Глаголы в различных грамматических формах чаще всего являются главным членом предложения — сказуемым.
Если правильно распределить время, ты многое успеешь .
Бабушка сидит на завалинке под окном.
Вернулся бы домой вовремя, да заблудился в лесу.
Видео:Совершенный вид глагола – что это такое понятным языком, чем он отличается от несовершенногоСкачать

Видеоурок «Глагол как часть речи»
Видео:Переставь одну цифру! Задача на логикуСкачать

Заключение
Об экспрессивных возможностях русского глагола говорили многие лингвисты и писатели. Еще Н. Греч отметил, что глагол «придает речи жизнь», «присутствием своим животворит отдельные слова».
Современные исследователи утверждают, что в глаголе, образно говоря, течет самая алая, самая артериальная кровь русского языка. Глагол во всем богатстве его семантики, со свойственными ему значениями грамматических форм и возможностями синтаксических связей, при многообразии стилистических приемов образного употребления является неисчерпаемым источником экспрессии.
Глагол — необыкновенная часть речи. В чем же заключается его сила?
Удивительным свойством русского глагола является его способность не только называть действие, но и показывать, как оно протекает во времени. А протекает оно необычайно разнообразно: может совершаться длительное время (прыгать, толкать, кричать, думать, слушать), но может произойти в один момент (прыгнуть, толкнуть, крикнуть, блеснуть), может обозначать начало действия (запеть, закричать, заболеть, загреметь) или, напротив, его конец (допеть, доварить, доделать, дописать, дочитать) и пр.
Важнейшая стилистическая функция глагола в речи – придавать динамизм описаниям. Глагол используется в речи прежде всего для передачи движения, выражающего динамику окружающего мира и духовной жизни человека.
Подведем итог словами К. Г Паустовского о русском языке:
С русским языком можно творить чудеса. Нет ничего такого в нашей жизни и в нашем сознании, что нельзя было бы передать русским словом. Звучание музыки, спектральный блеск красок, игру света, шум и тень садов, неясность сна, тяжёлое громыхание грозы, детский шёпот и шорох морского гравия. Нет таких звуков, образов и мыслей – сложных и простых, для которых не нашлось бы в нашем языке точного выражения.
Видео:Я В ШОКЕ😳Лайфхак, как умножать на пальцах 😎 Таблица умножения легкоСкачать

Математические действия на английском языке
Наиболее употребительные простые дроби.
Даже если ваша профессиональная деятельность никак не связана с точными науками, хотя бы основные математические действия на английском знать нужно. Они встречаются не только в специальной литературе, но и в фильмах, книгах, повседневной речи. В этой статье мы рассмотрим термины, связанные с арифметическими задачами, дробями, процентами. В конце я привожу озвученные карточки со основными словами на тему математики.
Обратите внимание, здесь рассматриваются только математические термины. Если вы ищете сведения о числительных, рекомендую эту статью: Числительные в английском языке.
Содержание:
Видео:Для тех кто идёт в 5-6 класс🌿 #shorts #школа #туториал #математика #урокСкачать

Основные математические действия на английском: сложение, вычитание, умножение и деление
Наиболее употребительные математические термины относятся к арифметике. Обратите внимание, в русском языке у нас есть такие слова, как:
- Сложение, вычитание, деление, умножение – название действия.
- Складывать, вычитать, делить, умножать – глагол, обозначающий действие.
- Плюс, минус, разделить, умножить – название действия, которое мы используем в речи, когда читаем выражение, именно оно используется чаще всего.
В английском языке точно так же, поэтому представим арифметические действия в виде таблицы:
Пройдите тест на уровень английского:
| Название действия (сущ.) | Название действия (глагол) | Используется в речи |
|---|---|---|
| Addition – сложение | Add – прибавлять | Plus – плюс |
| Subtraction – вычитание | Subtract – вычитать | Minus – минус |
| Multiplication – умножение | Multiply by – умножать на | Times – умножить |
| Division – деление | Divide by – делить на | Divided by – разделить |
| Equality – равенство | Equals to is equal to – равняться чему-то | Equals to is equal to is – равно |
Сама арифметическая задача (например, 2+2) называется problem (по-научному) или sum (разговорный вариант), решение или ответ – answer, а глагол “решать” – to solve (the problem).
- 2+2=4 – Two plus two equals four.
- 7-2=5 – Seven minus two equals five.
Часто вместо equals или is equal to говорят просто is.
- 5×3=15 – Five times three is fifteen.
- 8÷4=2 – Eight divided by four is two.
Дроби на английском языке
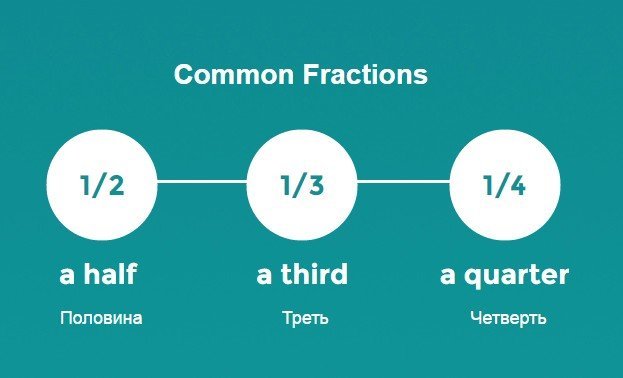
Простые дроби – common fractions
Если у вас с математикой так же “прекрасно”, как у меня, напомню самое основное о дробях.
Простые дроби (common fractions) состоят из числителя (numerator) и знаменателя (denominator). Напоминаю, числитель сверху, знаменатель снизу 🙂 Если число состоит из целого и дроби, например 1½, – это называется смешанная дробь или смешанное число (mixed numeral).
Числитель выражается количественным числительным, а знаменатель порядковым. Наиболее употребительные в речи дроби 1/2, 1/3, 1/4 в русском языке имеют не только “умные” называния “одна вторая”, “одна третья”, одна четвертая, но и простые: половина, треть, четверть. В английском точно так же.
- 1/2 – a half, one half.
- 1/3 – a third, one third.
- 1/4 – a quarter, one fourth.
- 1/5 – one fifth.
- 1/6 – one sixth.
- 2/3 – two thirds.
- 3/4 – three fourths.
- 1/8 – one eighth.
- 1/10 – a tenth.
- 1/100 – a hundredth.
- 1¼ – one and a quarter.
- 1½ – one and a half.
- 1¾ – one and three quarters.
Обратите внимание, когда числитель больше одного, к окончанию добавляется -s, так как знаменатель используется во множественном числе (как и в русском: две третьих, три четвертых).
Существительное, которое определяется дробью, используется с предлогом of:
- 3/4 mile – Three fourths of a mile.
- 1/4 bottle – A quarter of a bottle.
Существительное, определяемое смешанной дробью, используется без предлога, но во множественном числе:
- 2 ½ miles – Two and a half miles.
- 1¼ bottles – One and a quarter bottles.
Десятичные дроби – decimal fractions, decimals
В английском в десятичных дробях (decimals) целое от дроби отделяется точкой (point), а не запятой, как у нас.
Ноль перед точкой называется zero или (британский вариант) nought. Ноль после точки может называться oh (как буква “o”), zero, nought. Лично я для простоты всегда говорю zero, потому что это слово проще выговорить и расслышать. Если целое число в дроби равно нулю, его часто опускают в речи, начиная говорить сразу с “point”.
Целое число читается как обычное количественное числительное, например 45.1 – forty five point one. Но в дробной части каждая цифра читается отдельно тоже как количественное: 2.45 – two point four five (а не two point forty five).
- 0.1 – Point one, zero point one.
- 0.35 – Point three five, zero point three five.
- 1.25 – One point two five.
- 35.158 – Thirty five point one five eight.
- 15.05 – Fifteen point zero five.
Проценты в английском языке, трудности с числом глагола
Сотые доли могут выражаться с помощью процентов, тогда используется стандартный значок % и слово percent, всегда использующееся в единственном числе.
- 1% – One percent.
- 10% – Ten percent.
- 17% – Seventeen percent.
Трудность может вызвать число глагола в выражениях с процентами. Например:
- Twenty percent of the students are/is present. – 20% студентов присутствуют.
- The remaining twenty percent of the script has/have been rewritten. – Оставшиеся 20% сценария были переписаны.
В таких случаях глагол согласуется в числе с существительным после of:
- Twenty percent of the students are present (т. к. students – мн. число).
- The remaining twenty percent of the script has been rewritten (т. к. script – ед. число).
Возведение в степень в английском
Для обозначение степени используются выражения to the power of five, to the fifth power, raised to the power of five, raised to the fifth power. Для 2-ой и 3-ей степени используются термины “в квадрате” (squared) и “в кубе” (cubed).
- 3 2 – Three squared, three to the second power.
- 3 3 – Three cubed, three to the third power.
- 10 4 – Ten to the fourth power, ten to the power of four.
- 30 24 – Thirty to the power of twenty four.
Квадратный корень называется square root:
- √16 = 4 – The square root of sixteen is four.
- √25 = 5 – The square root of twenty five is five.
Математические выражения со скобками
Круглые скобки называются parentheses (ед. число parenthesis) или, проще, round brackets. Если выражение стоит в скобках, и к нему применяется операция, используется слово quantity.
- (2+3)×4=24 – Two plus three quantity times four equals to twenty four.
- (3+5) 2 =64 Three plus five quantity squared is sixty four.
Карточки с английскими словами на тему “Математика”
Математические термины из этой статьи можно выучить с помощью карточек на Quizlet и PDF-карточек для распечатки.