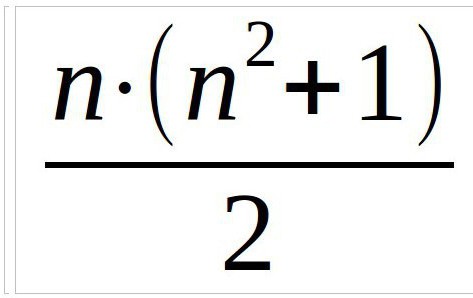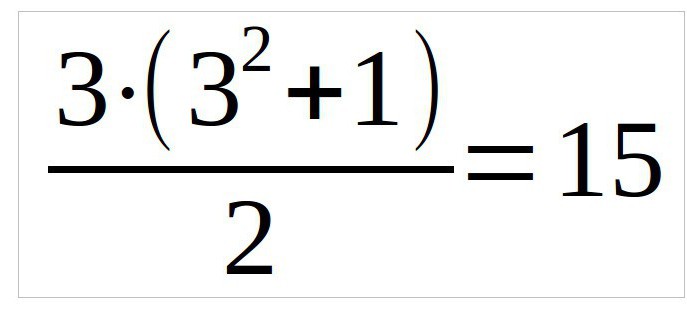Магический квадрат на спряжение глаголов (4 видео)

Как решить магический квадрат: учимся решать одну из древнейших задач

Магический квадрат представляет собой квадратную таблицу с числами, построенную так, что сумма чисел в каждой строке, каждом столбце и в каждой диагонали равна одному и тому же числу (магическая сумма). Магические квадраты бывают разных порядков — порядок квадрата определяет число столбцов/строк. Как рассчитать и решать магические квадраты?

Содержание

История
На уроках математики в школе
Один из способов решения магического квадрата
Как рассчитать магический квадрат Пифагора самому?
Решаем магический квадрат Пифагора: пример
Как решить магический квадрат (3 класс)? Пособия для школьников
Что это за загадка?
Какие есть решения
Первый способ. Когда квадрат нечетный
Второй способ. Для квадрата двойной четности
Третий способ. Для квадрата одинарной четности
Вывод
🎦 Видео

Видео:Решите задачу про магический квадрат за 1 минуту. Сможете?Скачать

История

Археологи нашли свидетельства того, что волшебные таблицы были известны еще древним грекам и китайцам. «Магическими» эти фигуры назвали арабы, которые наделяли их сверхъестественными защитными свойствами.

В середине XVI в. европейские математики занялись исследованиями загадочных таблиц, положив начало их новой жизни. Они искали общий метод построения магических квадратов и пытались описать все возможные их варианты.

Видео:Спряжение глаголов | Русский язык |TutorOnlineСкачать

На уроках математики в школе

Решение магических квадратов на уроках математики и внеклассных занятиях вызывает интерес, способствует развитию мышления. Дети учатся планировать и контролировать свою работу. В клетки магических квадратов можно записывать не только числа, но и выражения. Все зависит от изучаемой темы. Задания с магическими квадратами часто дают как дополнительные или олимпиадные уже в начальной школе.

Один из способов решения магического квадрата

Нетрудно решить магический квадрат третьего порядка (у которого по три столбца и строки). Можно воспользоваться тем фактом, что число (выражение), стоящее на пересечении его диагоналей, всегда равно ⅓ волшебной суммы. Отсюда следует алгоритм построения:

Вписываем в первую строку или столбец 3 любых числа.

Вычисляем магическую сумму (0 + 2 + 4 = 6).
Ищем ее третью часть (6/3 = 2).
Полученное число записываем на пересечении диагоналей.

Подбираем остальные числа и заполняем ими пустые клеточки квадрата.

Смотрите также:

Презентация "Магические квадраты"; 2 класс
Презентация "Магические квадрат"; 2-3 класс
Сценарий мероприятия "Магические квадраты и фокусы"; 5 класс

Видео:Спряжение глаголов. Как определить спряжение глаголов?Скачать

Как рассчитать магический квадрат Пифагора самому?

Пифагор — математик, заложивший основы нумерологии. Ученый верил, что миром правят числа. Даже человеческая сущность зависит от них, ведь дата рождения не что иное, как число.

Магический квадрат Пифагора — фигура третьего порядка, клетки которой заполнены числами от 1 до 9. Он делится на 3 уровня: материальный, души и разума.

Цифры даты рождения вписываются в определенном порядке. Полученная комбинация рассказывает о заложенных природой способностях человека.

Материал может быть использован на занятии математического кружка, на внеклассном мероприятии. Цель — развить и расширить познавательный кругозор и логическое мышление.

Решаем магический квадрат Пифагора: пример

Дата рождения: 17.09.2005 г. Складываем эти цифры, не учитывая нули: 1 + 7 + 9 + 2 + 5 = 24. Аналогично поступаем с цифрами результата: 2 + 4 = 6.

Из первой суммы вычитаем удвоенную первую цифру дня рождения: 24 -2 = 22. Снова складываем: 2 + 2 = 4. Полученные числа: 17; 9; 25; 24; 6; 22; 4.

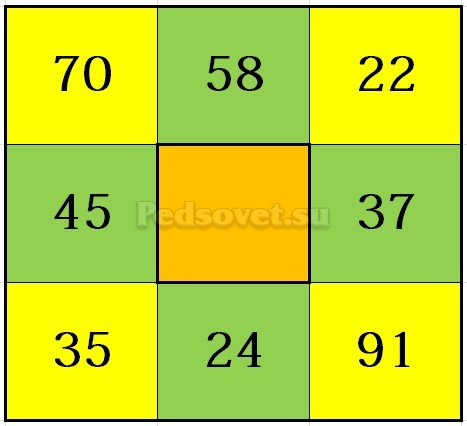
Цифры вписываем в магический квадрат так, чтобы все единицы оказались в первой клеточке, двойки — во второй и так далее. Нули не учитываем.

Клетка 1 – волевые качества, эгоизм.

Очень эгоистичные люди.

Эгоизм — яркая, но не преобладающая черта характера.

Спокойные, покладистые люди.

Сильный, волевой человек.

Люди с замашками диктатора.

Клетка 2 — биоэнергетика.

Воспитанность, природное благородство.

Люди с повышенной чувствительностью к атмосферным изменениям.

Человек с хорошим запасом биоэнергетики.

Клетка 3 — организованность, любовь к точности, конкретности, скрупулезность, скупость.

Чем больше троек, тем сильнее выражены вышеперечисленные качества.

Клетка 4 — здоровье.

Среднее, требуется закаливание.

Очень крепкое здоровье.

Клетка 5 — интуиция, экстрасенсорные способности

Чем больше пятерок, тем более выражена связь с космосом.

Клетка 6 — материализм.

Люди с неординарным воображением, которым необходим физический труд.

Могут посвятить время и творчеству, и точным наукам. Физические нагрузки обязательны.

Заземленные личности, тянущиеся к физическому труду.

Очень много заземленности.

Клетка 7 — талант.

Чем больше семерок, тем талантливее человек.

Клетка 8 — судьба, отношение к обязанностям.

Чувства долга нет.

Люди, которые всегда спешат помочь другим.

Признак служения народу.

Клетка 9 — умственные способности

Полное отсутствие девяток означает очень низкий уровень умственной деятельности. Чем больше количество девяток, тем умнее человек.

Задачи на составление магических квадратов часто включаются в сборники нестандартных заданий. Они встречаются на олимпиадах. Увлеченным математикой школьникам будет полезно узнать об этом классе задач.

Об авторе: Филиппова Оксана, учитель математики, физики и информатики.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями

Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст

Ошибка в тексте? Мы очень сожалеем,
что допустили ее. Пожалуйста, выделите ее
и нажмите на клавиатуре CTRL + ENTER.

Кстати, такая возможность есть
на всех страницах нашего сайта

0 Спам
1 LifeLana • 16:44, 01.02.2018

2007-2021 «Педагогическое сообщество Екатерины Пашковой — PEDSOVET.SU».
12+ Свидетельство о регистрации СМИ: Эл №ФС77-41726 от 20.08.2010 г. Выдано Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций.
Адрес редакции: 603111, г. Нижний Новгород, ул. Раевского 15-45
Адрес учредителя: 603111, г. Нижний Новгород, ул. Раевского 15-45
Учредитель, главный редактор: Пашкова Екатерина Ивановна
Контакты: +7-920-0-777-397, info@pedsovet.su
Домен: https://pedsovet.su/
Копирование материалов сайта строго запрещено, регулярно отслеживается и преследуется по закону.

Отправляя материал на сайт, автор безвозмездно, без требования авторского вознаграждения, передает редакции права на использование материалов в коммерческих или некоммерческих целях, в частности, право на воспроизведение, публичный показ, перевод и переработку произведения, доведение до всеобщего сведения — в соотв. с ГК РФ. (ст. 1270 и др.). См. также Правила публикации конкретного типа материала. Мнение редакции может не совпадать с точкой зрения авторов.

Для подтверждения подлинности выданных сайтом документов сделайте запрос в редакцию.

О работе с сайтом

Мы используем cookie.

Публикуя материалы на сайте (комментарии, статьи, разработки и др.), пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьми лицами.

При этом редакция сайта готова оказывать всяческую поддержку как в публикации, так и других вопросах.

Если вы обнаружили, что на нашем сайте незаконно используются материалы, сообщите администратору — материалы будут удалены.

Видео:Магические квадраты от моего Папы!Скачать

Как решить магический квадрат (3 класс)? Пособия для школьников

Математических загадок существует невообразимое количество. Каждые из них уникальны по-своему, но их прелесть заключается в том, что для решения неизбежно нужно приходить к формулам. Конечно же, можно попытаться решить их, как говорится, методом тыка, но это будет очень долго и практически безуспешно.

В данной статье будет говориться об одной из таких загадок, а чтобы быть точнее — о магическом квадрате. Мы детально разберем, как решить магический квадрат. 3 класс общеобразовательной программы, конечно, это проходит, но возможно не каждый понял или вовсе не помнит.

Видео:Как решать магический квадратСкачать

Что это за загадка?

Магический квадрат, или, как его еще называют, волшебный, — это таблица, в которой число столбцов и строк одинаково, и все они заполнены разными цифрами. Главная задача, чтобы эти цифры в сумме по вертикали, горизонтали и диагонали давали одинаковое значение.

Помимо магического квадрата, есть еще и полумагический. Он подразумевает то, что сумма чисел одинакова лишь по вертикали и горизонтали. Магический квадрат «нормальный» только в том случае, если для заполнения использовались натуральные числа от единицы.

Еще есть такое понятие, как симметричный магический квадрат — это когда значение суммы двух цифр равно, в то время, когда они располагаются симметрично по отношению к центру.

Важно также знать, что квадраты могут быть любой величины помимо 2 на 2. Квадрат 1 на 1 также считается магическим, так как все условия выполняются, хотя и состоит он из одного-единственного числа.

Итак, с определением мы ознакомились, теперь поговорим про то, как решить магический квадрат. 3 класс школьной программы вряд ли все так детально разъяснит, как эта статья.

Видео:Как правильно определить спряжение глаголов? Как пишутся окончания глаголов?Скачать

Какие есть решения

Те люди, которые знают, как решить магический квадрат (3 класс точно знает), сразу же скажут, что решения только три, и каждое из них подходит для разных квадратов, но все же нельзя обойти стороной и четвертое решение, а именно «наугад». Ведь в какой-то мере есть вероятность того, что незнающий человек все же сможет решить данную задачку. Но данный способ мы отбросим в длинный ящик и перейдем непосредственно к формулам и методикам.

Видео:Спряжение глаголов. Что такое спряжение глаголов в русском языке? Для чего нужно спряжение глаголов?Скачать

Первый способ. Когда квадрат нечетный

Данный способ подходит только для решения такого квадрата, у которого количество ячеек нечетное, например, 3 на 3 или 5 на 5.

Итак, в любом случае изначально необходимо найти магическую константу. Это число, которое получится при сумме цифр по диагонали, вертикали и горизонтали. Вычисляется она с помощью формулы:

В данном примере мы рассмотрим квадрат три на три, поэтому формула будет выглядеть так (n — число столбцов):

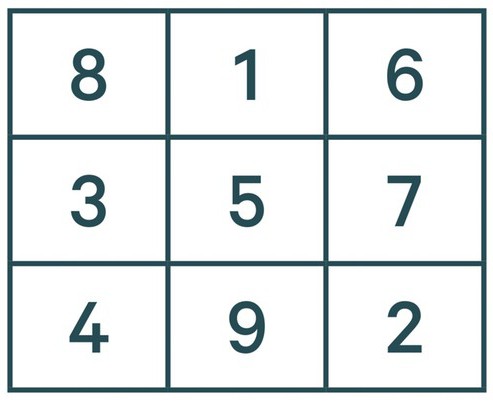
Итак, перед нами квадрат. Первое, что надо сделать — это вписать цифру один в центре первой строки сверху. Все последующие цифры необходимо располагать на одну клетку правей по диагонали.

Но тут сразу встает вопрос, как решить магический квадрат? 3 класс вряд ли использовал данный метод, да и у большинства появится проблема, как это сделать таким способом, если данной клетки нет? Чтобы сделать все правильно, необходимо включить воображение и дорисовать аналогичный магический квадрат сверху и получится так, что число 2 будет находиться в нем в нижней правой клетке. Значит, и в наш квадрат мы вписываем двойку в то же место. Это означает, что нам необходимо вписать цифры так, чтобы в сумме они давали значение 15.

Последующие цифры вписываются точно так же. То есть 3 будет находиться в центре первого столбца. А вот 4 по такому принципу вписать не удастся, так как на ее месте уже стоит единица. В таком случае цифру 4 располагаем под 3, и продолжаем. Пятерка — в центре квадрата, 6 — в правом верхнем углу, 7 — под 6, 8 — в верхний левый и 9 — по центру нижней строки.

Вы теперь знаете, как решить магический квадрат. 3 класс Демидова проходил, но у этого автора были чуть попроще задания, однако, зная данный способ, удастся разгадать любую подобную задачу. Но это, если число столбцов нечетное. А что же делать, если у нас, например, квадрат 4 на 4? Об этом дальше по тексту.

Видео:Спряжения глаголовСкачать

Второй способ. Для квадрата двойной четности

Квадратом двойной четности называют тот, у которого количество столбцов можно разделить и на 2, и на 4. Сейчас мы рассмотри квадрат 4 на 4.

Итак, как решить магический квадрат (3 класс, Демидова, Козлова, Тонких — задание в учебнике математики), когда количество его столбцов равно 4? А очень просто. Проще, чем в примере до этого.

В первую очередь находим магическую константу по той же формуле, что приводилась в прошлый раз. В данном примере число равно 34. Теперь надо выстроить цифры так, чтобы сумма по вертикали, горизонтали и диагонали была одинаковой.

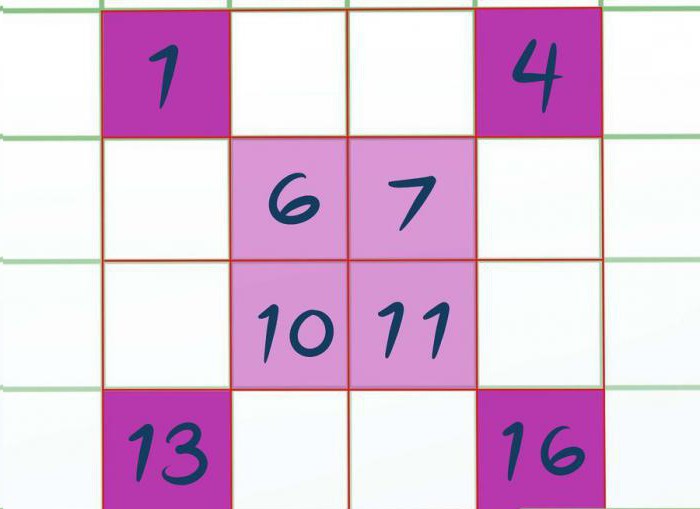
В первую очередь надо закрасить некоторые ячейки, сделать это вы можете карандашом или же в воображении. Закрашиваем все углы, то есть верхнюю левую клеточку и верхнюю правую, нижнюю левую и нижнюю правую. Если квадрат был бы 8 на 8, то закрашивать надо не одну клеточку в углу, а четыре, размером 2 на 2.

Теперь необходимо закрасить центр этого квадрата, так, чтобы его углы касались углов уже закрашенных клеточек. В данном примере у нас получится квадрат по центру 2 на 2.

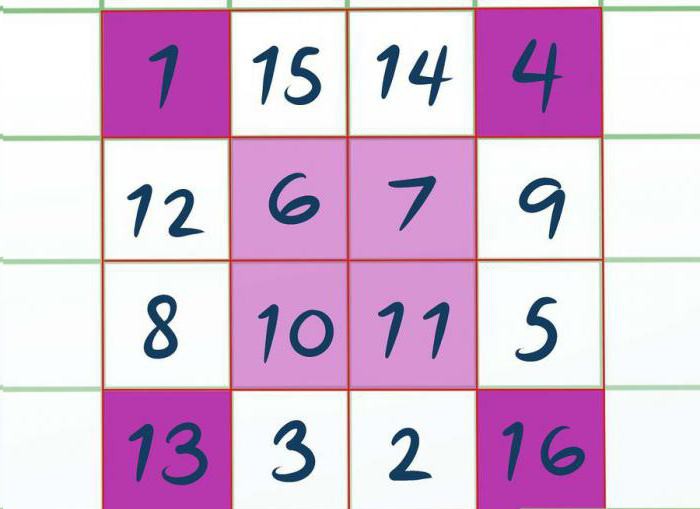
Приступаем к заполнению. Заполнять будем слева направо, в том порядке, в котором расположены ячейки, только вписывать значение будем в закрашенные клетки. Получается, что в верхний левый угол вписываем 1, в правый — 4. Потом центральный заполняем 6, 7 и дальше 10, 11. Нижний левый 13 и правый — 16. Думаем, порядок заполнения понятен.

Остальные ячейки заполняем точно так же, только в порядке убывания. То есть так как последняя вписанная цифра была 16, то вверху квадрата пишем 15. Далее 14. Потом 12, 9 и так далее, как показано на картинке.

Теперь вы знаете второй способ, как решить магический квадрат. 3 класс согласится, что квадрат двойной четности намного легче решается, чем другие. Ну а мы переходим к последнему способу.

Видео:Русский язык 5 класс (Урок№83 - Спряжение глаголов.)Скачать

Третий способ. Для квадрата одинарной четности

Квадратом одинарной четности называется, тот квадрат, число столбцов которого можно разделить на два, но нельзя на четыре. В данном случае это квадрат 6 на 6.

Итак, вычисляем магическую константу. Она равна 111.

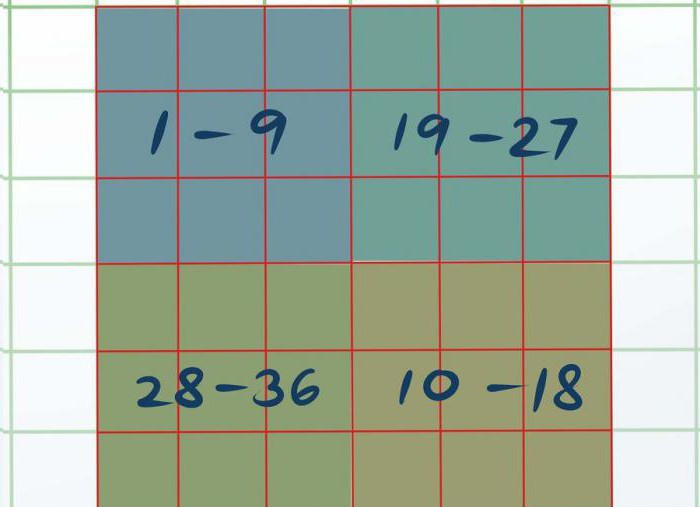
Теперь нужно наш квадрат визуально поделить на четыре разных квадрата 3 на 3. Получится четыре маленьких квадрата размером 3 на 3 в одном большом 6 на 6. Верхний левый назовем А, нижний правый — В, верхний правый — С и нижний левый — D.

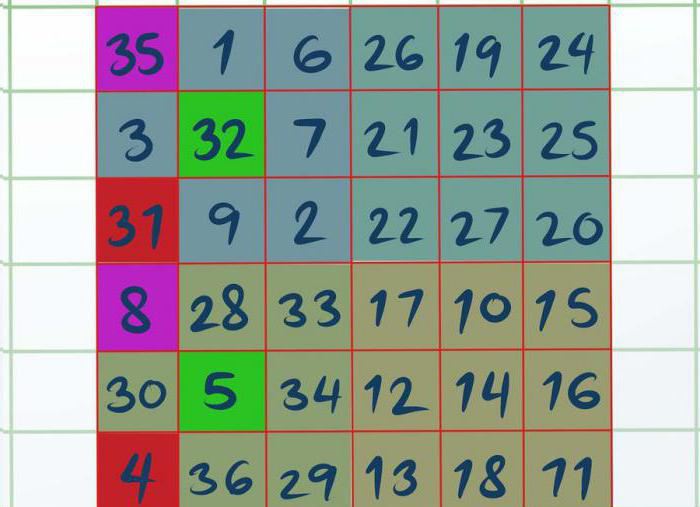
Теперь необходимо каждый маленький квадрат решить, используя самый первый способ, что приведен в этой статье. Получится так, что в квадрате А будут числа от 1 до 9, в В — от 10 до 18, в С — от 19 до 27 и D — от 28 до 36.

Как только вы решили все четыре квадрата, работа начнется над А и D. Необходимо в квадрате А визуально или при помощи карандаша выделить три ячейки, а именно: верхнюю левую, центральную и нижнюю левую. Получится так, что выделенные цифры — это 8, 5 и 4. Точно так же надо выделить и квадрат D (35, 33, 31). Все, что остается сделать, это поменять местами выделенные цифры из квадрата D в А.

Теперь вы знаете последний способ, как можно решить магический квадрат. 3 класс квадрат одинарной четности не любит больше всего. И это неудивительно, из всех представленных он самый сложный.

Видео:Как решать магические квадратыСкачать

Вывод

Прочтя данную статью, вы узнали, как решить магический квадрат. 3 класс (Моро — автор учебника) предлагает подобные задачи только с несколькими заполненными ячейками. Рассматривать его примеры нет смысла, так как зная все три способа, вы с легкостью решите и все предлагаемые задачи.